背景
之前周练考了,把叉乘乘反了,-9pts。
据说不咋考了,不过还是写一下,期末考 rp++ 触底反弹(
例题
借用周练题。
如图,y=−x6 上有两点 A(−2,3),B(6,−1),若点 P 在 y=−x6 上,且 S△APB=8,求点 P 坐标。
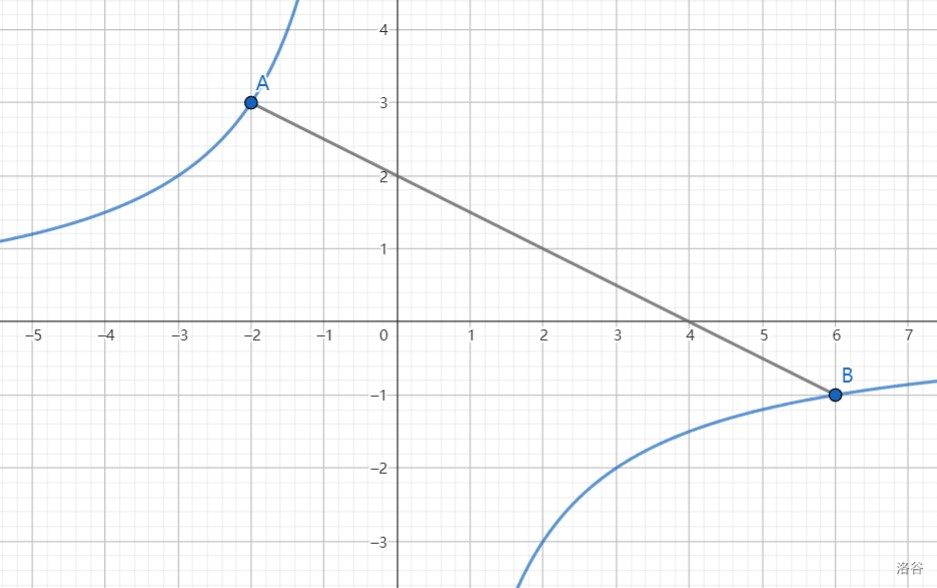
先设 P(x,−x6),并易得 yAB=−21x+2。
方法一:铅垂法
常规方法。我们先找一个点 P,过 P 竖割,如图:
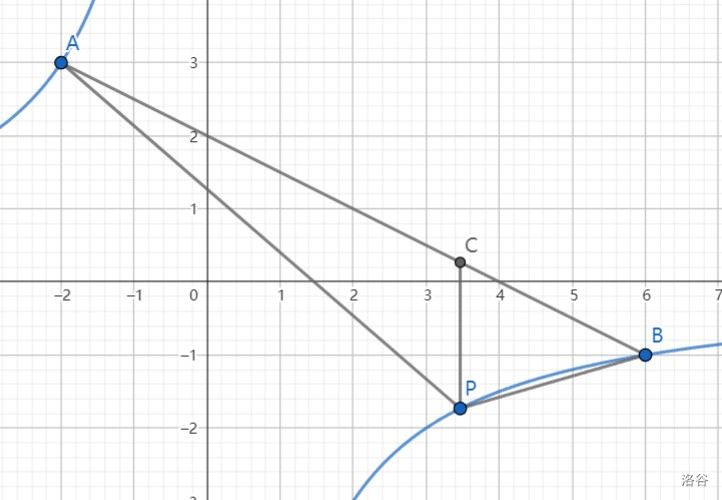
则 S△APB=S△ACP+S△BCP=21CP×h1+21CP×h2=21CP×∣xB−xA∣。
这个方法可以简记为:三角形面积是水平宽乘铅垂高的一半。
本题中,C(x,−21x+2),故 21×∣−21x+2−(−x6)∣×[6−(−2)]=8。
草稿纸在这里,最后可得答案:
P1(23,−3),P2(−23,3)P3(4+27,2−7),P4(4−27,2+7)
方法二:等积变形
考虑三角形的底是 AB=45,则顶点 P 对应的高 h=545。
由平行线间距离处处相等,作 l1,l2//AB,使距离为 h 即可。l1,l2 与 y=−x6 交于四点,这四点即为所求。
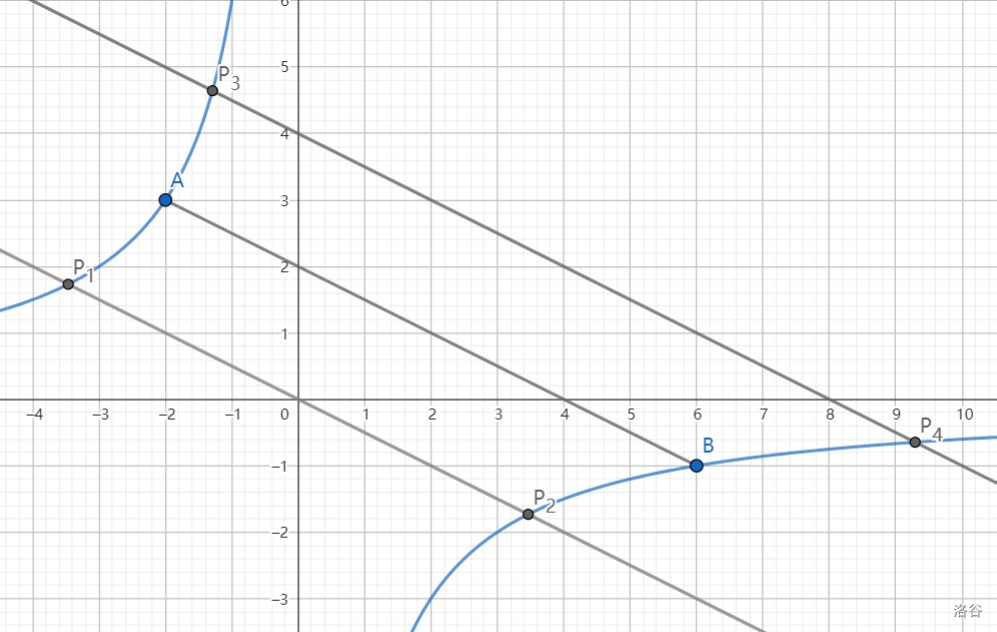
现在只需要求出 l1,l2 的方程联立即可。设 y=−21x+b,由平行线距离公式 k2+1∣b1−b2∣ 可得:
45∣b−2∣=545
这样解得 b1=0,b2=4,将 y=−21x 与 −21x+4 分别与 y=−x6 联立即可求得:
P1(23,−3),P2(−23,3)P3(4+27,2−7),P4(4−27,2+7)
方法三:作高法
直接过 P 作高,有 S△APB=21×AB×h。
应用点到直线距离公式 k2+1∣kx+b−y∣ 列方程:
21×45×45∣−21x+2−(−x6)∣=8
这个方程整理后与方法一一致,解得:
P1(23,−3),P2(−23,3)P3(4+27,2−7),P4(4−27,2+7)
方法四:公式法
唯 一 真 神。
应用向量叉乘,对于 A(x1,y1),B(x2,y2) 和原点围成的三角形,有公式:
S△AOB=21∣x1y2−y1x2∣
加入一点 C(x3,y3),变换坐标系,原点到 A 点,可得公式:
S△ABC=21∣(x3−x1)(y2−y1)−(y3−y1)(x2−y1)∣
这个公式笔者自己编了口诀:三减一乘二减一,减号两边 xy 换,绝对值再取一半。
在本题中,可列方程:
21∣−4(x+2)−8(−x6−3)∣=8
这个方程整理后与方法一一致,解得:
P1(23,−3),P2(−23,3)P3(4+27,2−7),P4(4−27,2+7)
总结
遇到无法直接算的三角形面积,可以采用铅垂法、等积变形、作高法、公式法解题。一般在坐标系中,三角形面积的存在性问题有多个答案,要注意分类讨论,合理取舍。


