引入
这是一道数据结构题。
维护一个数列,支持插入、删除、查排名、查数、前驱、后继。
以下,用 n n n w w w
Subtask 1:n ≤ 10 3 n \le 10^3 n ≤ 1 0 3
暴力 O ( n 2 ) O(n^2) O ( n 2 )
Subtask 2:n ≤ 10 4 n \le 10^4 n ≤ 1 0 4
采用 std::vector 和二分维护一个有序序列。由于 memmove 的小常数,可以卡常通过。
Subtask 3:n ≤ 10 5 , w ≤ 10 5 n \le 10^5, w \le 10^5 n ≤ 1 0 5 , w ≤ 1 0 5
权值线段树的模板。前驱后继用 std::map 维护即可,时空复杂度均为 O ( n log w ) O(n \log w) O ( n log w )
Subtask 4:n ≤ 10 5 , w ≤ 10 9 n \le 10^5, w \le 10^9 n ≤ 1 0 5 , w ≤ 1 0 9
把数字离散化后按 Subtask 3 的做法即可。
Subtask 5:n ≤ 10 5 , w ≤ 10 9 n \le 10^5, w \le 10^9 n ≤ 1 0 5 , w ≤ 1 0 9
这种时候就需要请出平衡树了。
平衡树的目的
引入 BST
首先,我们介绍一种数据结构,二叉搜索树(Binary Search Tree),简称 BST 。
让我们回顾二分查找的过程:
1 2 3 4 5 6 7 int l = 1 , r = n;while (l <= r) {int mid = (l + r) >> 1 ;if (a[mid] == target) return mid;if (a[mid] < target) l = mid + 1 ;else r = mid - 1 ;
如果我们维护 a a a O ( log n ) O(\log n) O ( log n )
但是,维护 a a a O ( n ) O(n) O ( n )
BST 的定义如下:
BST 是一棵二叉树,树中每个节点存储数值,数值不重;对于任意节点的孩子,其左孩子的值小于它的值,其右孩子的值大于它的值。
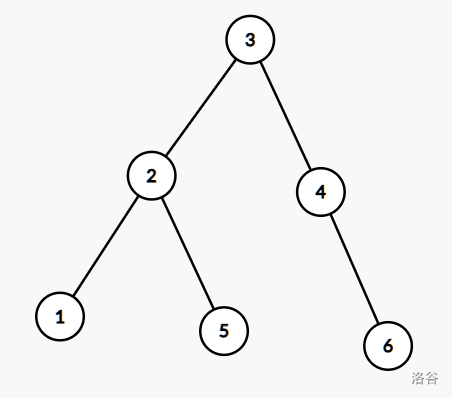
例如,把 1 , 2 , 3 , 4 , 5 , 6 1, 2, 3, 4, 5, 6 1 , 2 , 3 , 4 , 5 , 6
现在来考虑其他操作:
插入操作
BST 的结构十分适合二分。二分找到适合这个值的位置,新建节点即可。
如果要维护可重集,需要在节点中增加 cnt 域,如果节点存在则将 cnt 加一。由于 OI 中大部分情况需要维护可重集,下文默认 cnt 域的存在。
各种遍历
由于 BST 是二叉树,对其进行前序、中序、后序遍历都是可行的。BST 常用的是中序遍历。
BST 的性质:中序遍历一定有序。
简证:设 p p p l , r l, r l , r p p p l , p , r l, p, r l , p , r l < p < r l < p < r l < p < r
中序遍历参考实现如下,其余同理。
1 2 3 4 5 6 7 8 9 10 11 12 13 std::vector<T> inorder () const {if (!root) return {};reserve (size ());void (const node*)> dfs = [&](const node* x) -> void {if (!x) return ;dfs (x->left);for (int i = 1 ; i <= x->cnt; i++) res.emplace_back (x->val);dfs (x->right);dfs (root);return res;
特别地,为方便调试,我实现了一个 prettify 函数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 std::string prettify (int tabs = 4 , char fill = ' ' ) const {if (!root) return "" ;'(' << root->cnt << ")\n" ;for (int i = 1 ; i < tabs; i++) fill1. push_back (fill);for (int i = 1 ; i <= tabs; i++) fill2. push_back (fill);void (const node*, int , std::vector<int >)> dfs = const node* x, int depth, std::vector<int > sites) -> void {int void_num = 0 ;for (node* child : {x->left, x->right}) {if (!child) continue ;int n = depth - void_num - (int ) sites.size ();reserve (n << 1 );for (int i = 1 ; i <= n; i++) str_list.push_back ("│" + fill1);for (int site : sites) {insert (str_list.begin () + site, fill2);if (x->right && child != x->right) {emplace_back ("\u251c\u2500\u2500 " );else {emplace_back ("\u2514\u2500\u2500 " );push_back (depth);for (const std::string& s : str_list) out += s;'(' << child->cnt << ")\n" ;dfs (child, depth + 1 , sites);if (child == x->right) void_num--, sites.pop_back ();dfs (root, 0 , {});return ss.str ();
它的显示大概长这样:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 415495(0 )265337(1 )208361(1 )107323(1 )60423(1 )127077(1 )260553(1 )376755(1 )299181(1 )413857(1 )543050(1 )460416(1 )430219(1 )510033(1 )691707(1 )632641(1 )599175(1 )602133(1 )676499(1 )838037(1 )705510(1 )926433(1 )957395(1 )
查询操作
与插入类似,用一种类似二分的方法找到节点即可。
1 2 3 4 5 6 7 node* find (const T& val) const {while (cur && val != cur->val) {cmp (val, cur->val) ? cur->left : cur->right;return cur;
查询最值操作
根据 BST 中序遍历的性质,最小值是中序遍历的第一个数,最大值是中序遍历的最后一个数。
中序遍历的方法是左、中、右,所以最小值由根节点开始走左链,最大值由根节点开始走右链即可。
1 2 3 4 5 6 7 8 9 10 static node* get_min (node* cur) while (x && x->left) x = x->left;return x;static node* get_max (node* cur) while (x && x->right) x = x->right;return x;
前驱后继操作
先讲这个是为了理解删除。
一个数的前驱定义为 BST 中比他小的数的最大值。同理,一个数的后驱定义为 BST 中比他大的数的最小值。这个数不一定在 BST 中。有点类似 lower_bound 和 upper_bound。
以下只说前驱的实现,后继同理。
我们从根节点开始遍历,如果当前数比查询数小,则更新答案,并在右子树搜索;否则在左子树搜索。
思考这样为什么是对的:
答案小于查询数。由于我们在当前数比查询数小时更新答案,因此除非不存在任何一个比它小的数,否则答案一定小于查询数。
答案是小于查询数的最小值。在当前数比查询数小时往更大的右子树搜索可以保证这一点。
参考实现如下。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 T lower_bound (const T& val) const {T ();while (cur) {if (cmp (cur->val, val)) res = cur->val, cur = cur->right;else cur = cur->left;return res;T upper_bound (const T& val) const {T ();while (cur) {if (cmp (val, cur->val)) res = cur->val, cur = cur->left;else cur = cur->right;return res;
删除操作
BST 的删除比较复杂。 甚至比很多平衡树复杂。
先找到这个节点。设节点为 p p p
p p p c n t cnt c n t 1 1 1 c n t cnt c n t
若 p p p
若 p p p
若 p p p
对于情况 4 4 4
参考实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 bool remove_node (node*& cur) if (!cur) return false ;if (cur->cnt > 1 ) {pushup ();return true ;if (cur->left && cur->right) {this ->get_min (cur->right);1 ;remove (cur->right, replace->val);else {if (cur) cur->pushup ();return true ;bool remove (node*& cur, const T& val) if (!cur) return false ;if (val == cur->val) return remove_node (cur);bool res;if (cmp (val, cur->val)) res = remove (cur->left, val);else res = remove (cur->right, val);if (cur) cur->pushup ();return res;
排名相关
如果只有上面的操作,为什么不用 std::multiset 呢?这就要说到平衡树的重要操作——排名查询了。
平衡树模板题中将排名定义为比查询数小的数的个数 + 1 +1 + 1 0 0 0
如何实现排名操作?考虑权值线段树的做法。在每个节点维护一个 size,即这个子树中数的个数。这就需要维护 size 了。也许你看到上面的代码中有 pushup 操作,这就是维护 size 的操作。
1 2 3 4 BinarySearchTreeNode<T>* pushup () {0 ) + (right ? right->size : 0 );return this ;
根据数查询排名
从根节点搜到这个数,记录路径。
令 s s s c c c c n t cnt c n t
若在路径中向右搜了,则答案加上 s + c s+c s + c s + 1 s + 1 s + 1
这很适合递归。参考实现:
1 2 3 4 5 6 7 int rank (node* cur, const T& val) const if (!cur) return 1 ;int left_size = cur->left ? cur->left->size : 0 ;if (val == cur->val) return left_size + 1 ;if (cmp (val, cur->val)) return rank (cur->left, val);return rank (cur->right, val) + left_size + cur->cnt;
根据排名查询数
上述操作逆过来即可。
1 2 3 4 5 6 7 T kth (node* cur, int k) const {if (!cur) return T ();int left_size = cur->left ? cur->left->size : 0 ;if (left_size >= k) return kth (cur->left, k);if (left_size < k - cur->cnt) return kth (cur->right, k - left_size - cur->cnt);return cur->val;
建树
简单说一下,在替罪羊的重构有用。实际上很少这么做。
令序列为 a a a
如果当前处理的区间为 [ l , r ] [l,r] [ l , r ] m i d = ⌊ l + r 2 ⌋ mid=\lfloor \dfrac{l+r}{2} \rfloor mi d = ⌊ 2 l + r ⌋ a m i d a_{mid} a mi d [ l , m i d − 1 ] [l,mid-1] [ l , mi d − 1 ] [ m i d + 1 , r ] [mid+1,r] [ mi d + 1 , r ]
建树是 O ( n ) O(n) O ( n ) O ( n log n ) O(n \log n) O ( n log n ) O ( n log n ) O(n \log n) O ( n log n )
完整实现
BST 完整实现
应用
平衡树最大的应用是维护有序集合。或者说,我们给 std::multiset 添加了 O ( log n ) O(\log n) O ( log n )
除此之外,由于 splay 和 fhq-treap 的一些特性,平衡树可以用来支持区间操作。splay 是 LCT 的基础。
优化
你遇到了数据随机的平衡树模板。你敲了 BST 上去,A 掉了这道水题。
你遇到了加强版。听取 TLE 声一片。
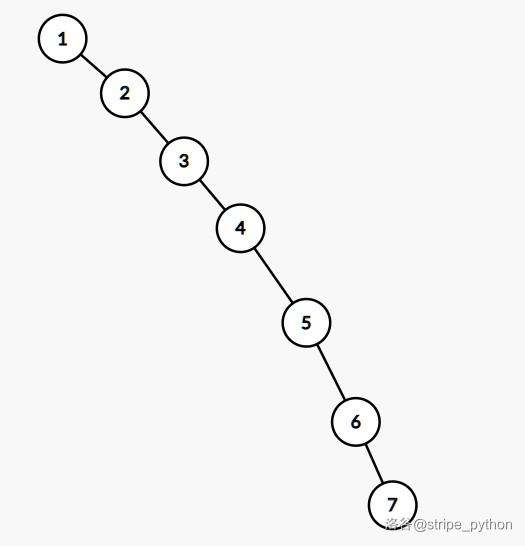
注意到,BST 在最坏情况下会退化为一个有序链表。例如,执行下面的操作:
1 insert (1 , 2 , 3 , 4 , 5 , 6 , 7 );
BST 的形态如下:
如果维护有序链表,复杂度和暴力相同,是 O ( n ) O(n) O ( n )
可以证明,在随机数据下,BST 的期望树高是 O ( log n ) O(\log n) O ( log n ) O ( h ) O(h) O ( h ) h h h h h h O ( n ) O(n) O ( n )
AVL
根据上面的思路,可以引出 AVL。
AVL 的每个节点维护一个 high 域,表示子树的高度。AVL 需要维护 ∣ h i g h l − h i g h r ∣ ≤ 1 |high_l-high_r|\le 1 ∣ hi g h l − hi g h r ∣ ≤ 1
左旋右旋的引入
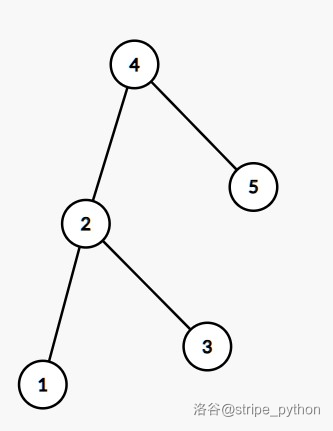
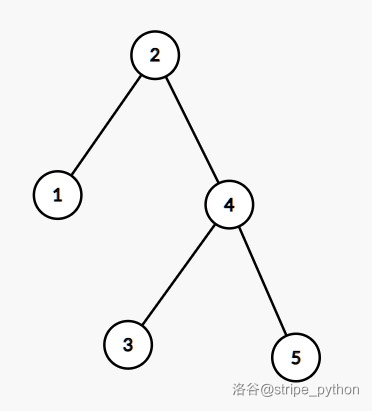
注意到,对一棵 BST 结构进行调整是不影响树的合法性的。举个例子:
这棵 BST 可以调整为:
这就是平衡树的左旋操作。类似地,把上述调整的逆过程称作右旋。
参考代码:
1 2 3 4 5 6 7 8 9 10 static node* left_rotate (node* p) pushup ();return q->pushup ();static node* right_rotate (node* p) pushup ();return q->pushup ();
如何维护平衡
分类讨论破坏平衡的情况:
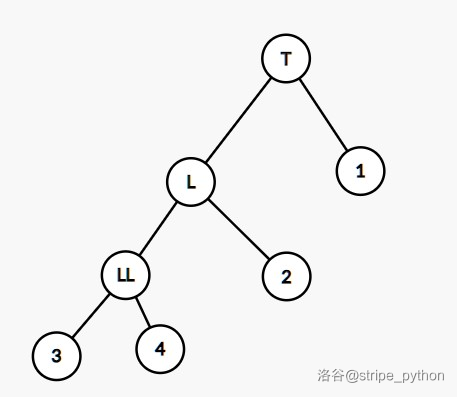
LL 型(左孩子的左孩子过深),如图:
解法:右旋节点 T T T
RR 型(右孩子的右孩子过深),解法:类似 LL 型,左旋节点 T T T
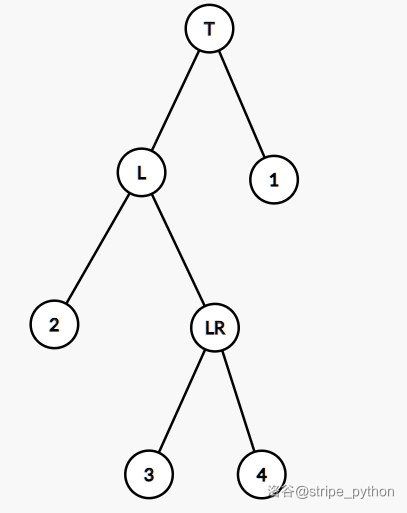
LR 型(左孩子的右孩子过深),如图:
解法:左旋节点 L,成为 LL 型,后右旋节点 T,即左右双旋。
RL 型(右孩子的左孩子过深),解法:类似 LR 型,右旋节点 R R R T T T
双旋的参考实现:
1 2 3 4 5 6 7 8 static node* left_right_rotate (node* p) right_rotate (p->left);return left_rotate (p);static node* right_left_rotate (node* p) left_rotate (p->right);return right_rotate (p);
代码修改
首先,加入一个 get_high 函数防止空指针。
1 static long get_high (node* p) return p ? p->high : 0 ;}
修改 insert 操作
1 2 3 4 5 6 7 8 9 10 11 12 13 if (cmp (val, cur->val)) {insert (cur->left, val), cur->pushup ();if (get_high (cur->left) - get_high (cur->right) >= 2 ) {cmp (val, cur->left->val) ? left_rotate (cur) : left_right_rotate (cur);else {insert (cur->right, val), cur->pushup ();if (get_high (cur->right) - get_high (cur->left) >= 2 ) {cmp (val, cur->right->val) ? right_left_rotate (cur) : right_rotate (cur);
改动搜索部分,调整平衡。
修改 remove 操作
remove 相对难改一点。为了方便,我把代码全部展示出来,添加的代码用注释标注。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 bool remove_node (node*& cur) if (!cur) return false ;if (cur->cnt > 1 ) {pushup ();return true ;if (cur->left && cur->right) {this ->get_min (cur->right);1 ;remove (cur->right, replace->val), cur->pushup ();if (get_high (cur->left) - get_high (cur->right) >= 2 ) { get_high (cur->left->left) >= get_high (cur->left->right)) ? left_rotate (cur) : left_right_rotate (cur); else {if (cur) cur->pushup ();return true ;bool remove (node*& cur, const T& val) if (!cur) return false ;if (val == cur->val) return remove_node (cur);bool res;if (cmp (val, cur->val)) {remove (cur->left, val), cur->pushup ();if (get_high (cur->right) - get_high (cur->left) >= 2 ) { get_high (cur->right->right) >= get_high (cur->right->left) ? right_rotate (cur) : right_left_rotate (cur); else {remove (cur->right, val), cur->pushup ();if (get_high (cur->left) - get_high (cur->right) >= 2 ) { get_high (cur->left->left) >= get_high (cur->left->right) ? left_rotate (cur) : left_right_rotate (cur); if (cur) cur->pushup ();return res;
其他操作和 BST 毫无区别。
完整实现
AVL 完整实现
闲谈
AVL 的常数比较大。但是,对于 OI 中常用的平衡树(Splay 和 Treap),它的性能还是比较好的。
其实我个人比较喜欢 AVL。AVL 只要把 BST 写出来了基本上就不会写挂,码量比起 BST 也就增加了五十行。而且 AVL 的节点调整有种解魔方的感觉,记住了基本挂不了。
AVL 的最大优势是查询。AVL 只在修改时作旋转,所以 AVL 的查询跑得飞快。
Treap
定义
Treap 是 BST 与堆的结合。具体来说,Treap 是堆关键字随机的笛卡尔树。
Treap 的节点额外定义了 prio 域,初始化为随机值。Treap 的每个节点除了满足 BST 的定义外,还要保证父节点的 prio 小于孩子的 prio。即:val 上维护 BST 性质,prio 上维护小根堆性质。
可以证明,这样做的复杂度是期望 O ( log n ) O(\log n) O ( log n )
性质维护
如何维护 prio 的性质?
把 AVL 的左旋右旋抄过来:
1 2 3 4 5 6 7 8 9 10 11 12 static node* left_rotate (node* p) pushup ();return p->pushup ();static node* right_rotate (node* p) pushup ();return p->pushup ();
填加一个 get_prio 函数防止空指针:
1 static long get_prio (node* cur) return cur ? cur->prio : 0 ;}
其实,Treap 的核心维护就是这两种逻辑:
当左子树的 prio 小于当前节点的,进行右旋;
当右子树的 prio 小于当前节点的,进行左旋。
1 2 if (get_prio (cur->left) < get_prio (cur)) cur = right_rotate (cur);if (get_prio (cur->right) < get_prio (cur)) cur = left_rotate (cur);
修改 insert 函数如下:
1 2 3 4 5 6 7 8 9 10 11 void insert (node*& cur, const T& val) if (cmp (val, cur->val)) {insert (cur->left, val), cur->pushup ();if (get_prio (cur->left) < get_prio (cur)) cur = right_rotate (cur);else {insert (cur->right, val);if (get_prio (cur->right) < get_prio (cur)) cur = left_rotate (cur);pushup ();
对于删除操作,除了 BST 的分类讨论,还要根据 prio 让 prio 小的当父节点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 bool remove_node (node*& cur) if (!cur) return false ;if (cur->cnt > 1 ) {pushup ();return true ;if (cur->left || cur->right) {if (!cur->right || get_prio (cur->left) > get_prio (cur->right)) {right_rotate (cur);remove (cur->right, val);else {left_rotate (cur);remove (cur->left, val);return cur->pushup (), true ;return cur = nullptr , true ;
这个删除甚至比 BST 简单。
完整实现
Treap 实现
闲谈
有旋 Treap 好像工程应用不多,但在 OI 中是应用最多的平衡树之一。实现了 BST 可以很方便地实现 Treap,而且 Treap 常数小,值得学习。
Treap 的另一个优点是它可持久化,可单调栈 O ( n ) O(n) O ( n )
FHQ-Treap
FHQ-Treap 又称无旋 Treap,是 OI 界平衡树的主力。
优缺点
在 FHQ-Treap 前,先了解一下优缺点:
优点:
码量非常少(甚至少写点功能能比 BST 还少)
不容易写挂
支持区间操作
支持可持久化
天然支持分裂、合并
支持线性建树
缺点:
常数大(常用平衡树里最慢的)
维护 LCT 不如 Splay 优秀(多了一个 log \log log
总的来说,FHQ-Treap 还是值得学习的。
性质维护
如它的名字,FHQ-Treap 满足 Treap 的性质。但是,FHQ-Treap 采用不同的性质维护方法——分裂和合并。这就是它为什么可以维护区间操作。
分裂
其实 BST 这种数据结构天然支持分裂。我们实现两个函数,lower_split 表示把小于查询值和大于等于查询值的树分裂,upper_split 表示把小于等于查询值和大于查询值的树分裂。
注:市面上常见的 FHQ-Treap 写法是用 lower_split(x - 1) 替代 upper_split(x)。这样可以减少码量,但我本人喜欢这么写。
考虑如何实现 lower_split,令 lower_split 返回分裂后的两棵树。根据查询值搜索:
当前值大于等于查询值。此时,当前节点的右子树的全部值大于查询值,归入第二棵树,对左子树进行分裂即可。
当前值小于查询值。此时,当前节点的左子树的全部值小于查询值,归入第一棵树,对右子树进行分裂即可。
upper_split 将分类讨论中的大于等于改为大于,小于改为小于等于即可。
在常用实现中,由于 C++14 不支持解包,用引用返回两棵树比较方便。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 void lower_split (node* cur, const T& val, node*& x, node*& y) if (!cur) return (void ) (x = nullptr , y = nullptr );if (!cmp (val, cur->val)) { lower_split (x->right, val, x->right, y);pushup ();else {lower_split (y->left, val, x, y->left);pushup ();void upper_split (node* cur, const T& val, node*& x, node*& y) if (!cur) return (void ) (x = nullptr , y = nullptr );if (val != cur->val && !cmp (val, cur->val)) { upper_split (x->right, val, x->right, y);pushup ();else {upper_split (y->left, val, x, y->left);pushup ();
合并
合并操作是 FHQ-Treap 的重点。合并有点类似线段树的合并,但要维护 Treap 的堆性质。可以证明,这样做的期望时间复杂度是 O ( log n ) O(\log n) O ( log n )
合并函数接收两棵树,其中第一棵树的所有值小于第二棵树的所有值。合并时,只需将 prio 小的上提,递归合并其子树即可。
1 2 3 4 5 6 7 8 9 10 node* merge (node* x, node* y) {if (!x || !y) return x ? x : y;if (x->prio < y->prio) {merge (x->right, y);return x->pushup ();else {merge (x, y->left);return y->pushup ();
操作维护
插入操作
理论上,插入操作可以抄 Treap 的。但是,既然写了 FHQ-Treap,有更简单的办法。
我们把整棵树按插入值 lower_split 成两部分,则第一棵树中所有值小于等于插入值,第二棵树中所有值大于插入值,在两棵树之间新建节点,合并即可。
需要注意,FHQ-Treap 为简便可以不维护 cnt 域,挂重复节点即可。
1 2 3 4 5 6 7 8 void insert (const T& val) if (!root) {new node (val);return ;lower_split (root, val, x, y); merge (merge (x, new node (val)), y);
删除操作
按删除值 split 成三段:小于删除值的、等于删除值的、大于删除值的。删除等于删除值的节点即可。
1 2 3 4 5 6 7 8 9 bool remove (const T& val) lower_split (root, val, x, z); upper_split (x, val, x, y);if (!y) return false ;merge (y->left, y->right);merge (merge (x, y), z);return true ;
查询排名
按查询值 upper_split。由于排名是比它小的数的数量,查第一棵树的 size 即可。
1 2 3 4 5 6 int rank (const T& val) upper_split (root, val, x, y); int rnk = x ? x->size : 0 ;merge (x, y);return rnk;
完整实现
FHQ-Treap 完整实现
闲谈
FHQ-Treap 非常好写,还可持久化,可维护区间,也很好学。
但是它的常数很大,使用时,需要注意时限。同时,FHQ-Treap 也可以维护 cnt 域(见 OI-Wiki 的实现),使平衡树结构更为严谨。
Splay
大多数 OI 选手学习的平衡树。支持区间操作和维护 LCT,本身常数较大,不支持可持久化。
性质维护
Splay 维护平衡的操作很简单:每一个被访问的节点都旋转到根。这一操作即 splay 操作。复杂度证明见 OI-Wiki 。
splay 操作基于左旋和右旋操作。可以去 AVL 树看一看。
splay 操作中的每次旋转是一次 splay 步骤。splay 步骤的目的是把该节点旋转到距离根更近的位置。
我们令该节点为 x x x f a fa f a g g g
f a fa f a x x x f a fa f a f a , x , g fa,x,g f a , x , g g g g x x x f a fa f a f a , x , g fa,x,g f a , x , g x x x
通过这些步骤,可以完成 splay。代码比想象的精简很多,利用奇偶可以方便地完成。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 static void rotate (node*& x) nullptr ;bool chk = x->get ();child (chk) = x->child (chk ^ 1 );if (x->child (chk ^ 1 )) x->child (chk ^ 1 )->parent = y;child (chk ^ 1 ) = y;if (z) z->child (y == z->right) = x;pushup (), x->pushup ();node* splay (node*& x) {for (node* fa = x->parent; (fa = x->parent); rotate (x)) {if (fa->parent) rotate (x->get () == fa->get () ? fa : x);return root = x;
修改 insert 操作
为了 insert 以后还能 splay,我们采用迭代实现。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void insert (const T& val) if (!root) {new node (val);return ;nullptr ;while (cur) {if (cur && val == cur->val) {pushup (); if (fa) fa->pushup ();splay (cur);return ;cmp (val, cur->val) ? cur->left : cur->right;new node (val), cur->parent = fa;if (cmp (val, fa->val)) fa->left = cur;else fa->right = cur;pushup (), fa->pushup ();splay (cur);
修改 remove 操作
前置知识:如何合并两棵 splay 树?第一棵树的所有元素小于第二棵的所有元素。
我们只需要把第一棵树中的最大值 splay 到根,将其右孩子设置为第二棵树的根即可。
把该节点 splay 到根。分类讨论:
单节点,直接删除;
缺一个孩子,将另一个上提替代;
有两个孩子,合并两棵子树即可(看看前置知识)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 bool remove (const T& val) if (!splay (val)) return false ;if (cur->cnt > 1 ) {pushup ();return true ;if (!cur->left && !cur->right) {delete cur;nullptr ;return true ;if (!cur->left) {nullptr ;else if (!cur->right) {nullptr ;else {root_pre ();pushup ();delete cur;return true ;
其他还有一些修改。看代码即可理解。
Splay 完整实现
闲谈
Splay 的结构使其容易维护区间操作。维护 LCT 时也常用这种平衡树的魔改版(甚至码量还更小)。
但是常数确实大(也许是我实现的原因),和 FHQ-Treap 差不多了。
其他平衡树
替罪羊树
如果失衡就暴力重构。复杂度均摊 O ( log n ) O(\log n) O ( log n )
WBLT
其实这东西已经不是 BST 了。
一种 Leafy Tree,常数小,可以维护区间操作,支持可持久化,是好东西。没看懂。
红黑树
工程中平衡树的主力,常数小。本质是 B 树变形。没看懂。
红黑树有一些变形,如左偏红黑树或 AA 树。码量也较多。
平衡树的替代品
这一部分简要介绍一下与 BST 无关的数据结构或 C++ 的内置数据结构。
块状链表
整体复杂度是 O ( n n ) O(n \sqrt{n}) O ( n n )
思想就是链表套分块,用一个 list<vector<T>> 就可以很方便地维护,整体维护有序。代码量比平衡树小很多。
在块内大小超过 n \sqrt{n} n
1 2 lst.emplace (next (it), it->begin () + (lim >> 1 ), it->end ());erase (it->begin () + (lim >> 1 ), it->end ());
块状链表完整实现
01-Trie
把数字二进制分解,用字典树维护,本质是值域为 2 w 2^w 2 w log \log log
这篇题解 使用类似后缀树的方法将空间压缩到了线性。这样 01-Trie 就能对标平衡树操作了。还能可持久化。
C++ 内置
__gnu_pbds::tree
pbds 实现了一个平衡树,采用红黑树或 Splay 树。在编写可重平衡树时,使用如下:
1 2 3 4 5 #include <ext/pb_ds/assoc_container.hpp> #include <ext/pb_ds/tree_policy.hpp> using namespace __gnu_pbds;int >, null_type, less<pair<T, int >>, rb_tree_tag, tree_order_statistics_node_update> tr;
pair 的第一个元素存储数据,第二个元素该元素的标号,以维护可重。
详情见 OI Wiki ,不再赘述。
__gnu_cxx::rope
pbds 的“块状链表”实现。实际上,rope 的内部实现是可持久化平衡树,这使它天然支持可持久化。但是,rope 常数和空间大,比赛慎用。
1 2 3 4 #include <ext/rope> using namespace __gnu_cxx;
具体使用见 OI Wiki 。
Sorted Containers
sortedcontainers 是 Python3 的第三方库,可以实现普通平衡树的功能。
sortedcontainers 实现了 SortedList,支持各类平衡树的操作。据说复杂度是均摊 O ( log n ) O(\log n) O ( log n )
具体方法比较复杂,可以看 这篇知乎讨论 。我试着实现一个 sorted_vector,最后放弃了。(因为 sortedcontainers 的 Pythonic 拿 C++ 写太难受了)
去平衡树模板题交了几发,发现它根本不像市面上说的与 C++ 速度相当,反而跑得飞慢(也许是 python 的读入慢)。加强版更是听取 TLE 声一片。
测试
叠甲:所有测试结果的实现代码均为本人自己的实现(平衡树全部用指针,替罪羊树 α = 0.75 \alpha=0.75 α = 0.75
P3369 普通版
数据结构
总运行时间
AVL
195ms
Treap
213ms
权值线段树
247ms
FHQ-Treap
254ms
Splay
289ms
块状链表
451ms
P6136 加强版
数据结构
总运行时间
AVL
10.10s
Treap
13.52s
Splay
15.32s
FHQ-Treap
16.20s
权值线段树
无法通过(离线算法)
块状链表
无法通过(TLE)