浅谈一种黑科技--索引树优化块状链表

众所周知，块状链表实现平衡树是 O(nn)O(n\sqrt{n}) 的，且不用一些手段卡不过加强版，那么有没有什么科技可以让块链达到 O(nlog⁡n)O(n \log n) 呢？

有的兄弟，有的。在 Python 的第三方库 Sorted Containers 里实现了一种块状链表，通过建索引树倍增优化查找过程，使得单次操作的复杂度降到了均摊 O(log⁡n)O(\log n)。

这种块链跑的飞快，在 mmap 快读加持下直接跑到平衡树加强版的次优解，C++ 的最优解。下面我们来讲解索引树优化块状链表的方法。其实这玩意就是单层跳表。

实现

阅读这里的 Python 代码需要一定的 Python 基础和 Pythonic 技巧。 如果您不会 Python，可以直接看 C++ 版实现。

首先你要下载 sortedcontainers 库，然后打开 sortedlist.py 阅读源码。

内部结构

先找到 SortedList 类，我们看看它的 __init__ 函数：

1
2
3
4
5
6
7
8
9
10
11
def __init__(self, iterable=None, key=None):
    assert key is None
    self._len = 0
    self._load = self.DEFAULT_LOAD_FACTOR
    self._lists = []
    self._maxes = []
    self._index = []
    self._offset = 0

    if iterable is not None:
        self._update(iterable)

参考这篇知乎回答，我们来看看这些变量都是什么：

  • _len：列表的长度；
  • _load：类似于块长，当块长大于二倍时分裂，小于一半时合并。sortedcontainers 里的默认块长 DEFAULT_LOAD_FACTOR 是 10001000，本蒟蒻实测 C++ 取 340340 效率较好。
  • _lists：就是块状链表，由于 list 的插入删除常数很小，直接用 list 套 list 实现，它里面的每个列表都要有序。
  • _maxes：块内最大值。这样我们可以二分找到元素所属块。
  • _index：索引树，我们稍后讲解。
  • _offset：偏移量，与索引树的层数有关。

分析完这些后，我们可以写出 C++ 版的代码：

1
2
3
4
5
6
7
8
9
10
11
12
template <class T>
struct sorted_vector {
private:
	static constexpr int DEFAULT_LOAD_FACTOR = 340;
	int len, load, offset;
	std::vector<std::vector<T>> lists;
	std::vector<T> maxes, index;
public:
	sorted_vector() : len(0), load(DEFAULT_LOAD_FACTOR), offset(0) {}
	int size() const {return len;}
	bool empty() const {return maxes.empty();}
};

索引树

索引树的构建方法是，以这些块的长度为叶子节点，自顶向上两两合并。例如对于 [[1, 2, 3], [4, 5], [6, 7, 8, 9], [10, 11, 12, 13, 14]]，我们建立的索引树如图：

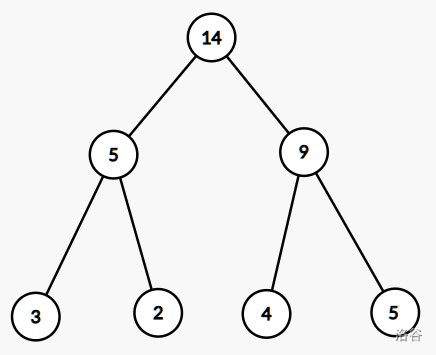
这是个 Leafy Tree。因为这玩意是个满二叉树，可以堆式存储，而 _offset 维护的就是叶子节点的开始下标，在这里就是 33。

我们写出 C++ 版本的建树代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
std::vector<int> parent(const std::vector<int>& a) {
    int n = a.size();
    std::vector<int> res(n >> 1);
    for (int i = 0; i < (n >> 1); i++) res[i] = a[i << 1] + a[i << 1 | 1];
    return res;
}
void build_index() {
    std::vector<int> row0;
    for (const auto& v : lists) row0.emplace_back(v.size());
    if (row0.size() == 1) return index = row0, offset = 0, void();
    std::vector<int> row1 = parent(row0);
    if (row0.size() & 1) row1.emplace_back(row0.back());
    if (row1.size() == 1) {
        index.emplace_back(row1[0]);
        for (int i : row0) index.emplace_back(i);
        return offset = 1, void();
    }
    int dep = 1 << (std::__lg(row1.size() - 1) + 1), u = row1.size();
    for (int i = 1; i <= dep - u; i++) row1.emplace_back(0);
    std::vector<std::vector<int>> tree = {row0, row1};
    while (tree.back().size() > 1) tree.emplace_back(parent(tree.back()));
    for (int i = tree.size() - 1; i >= 0; i--) index.insert(index.end(), tree[i].begin(), tree[i].end());
    offset = (dep << 1) - 1;
}

Python 版本建树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def _build_index(self):
    row0 = list(map(len, self._lists))

    if len(row0) == 1:
        self._index[:] = row0
        self._offset = 0
        return

    head = iter(row0)
    tail = iter(head)
    row1 = list(starmap(add, zip(head, tail)))

    if len(row0) & 1:
        row1.append(row0[-1])

    if len(row1) == 1:
        self._index[:] = row1 + row0
        self._offset = 1
        return

    size = 2 ** (int(log(len(row1) - 1, 2)) + 1)
    row1.extend(repeat(0, size - len(row1)))
    tree = [row0, row1]

    while len(tree[-1]) > 1:
        head = iter(tree[-1])
        tail = iter(head)
        row = list(starmap(add, zip(head, tail)))
        tree.append(row)

    reduce(iadd, reversed(tree), self._index)
    self._offset = size * 2 - 1

首先建叶子层使用了 map 函数，它类似于 C++ 中的 std::for_each，对于每个范围内的元素作 len 操作，这样就得到了叶子节点。接下来这几行代码：

1
2
3
head = iter(row0)
tail = iter(head)
row1 = list(starmap(add, zip(head, tail)))

zip 的作用是把 head 和 tail 压到一起，由于这里 head 和 tail 指向同一个迭代器，因此 zip(head, tail) 是两两交替的。starmap 函数是 map 的二元版本，通过这种操作，我们就得到了倒数第二层。之后建树同理。

1
reduce(iadd, reversed(tree), self._index)

通过一行代码就实现了将 tree 中的元素翻转后，不断加到 _index 上。

位置操作

这里的位置操作有两种，分别是 loc 和 pos。loc 操作是将形如第几个块的第几个元素转换为整个列表的第几个元素，pos 则相反。我们先来看 pos 操作：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def _pos(self, idx):
    if idx < 0:
        last_len = len(self._lists[-1])

        if (-idx) <= last_len:
            return len(self._lists) - 1, last_len + idx

        idx += self._len

        if idx < 0:
            raise IndexError('list index out of range')
    elif idx >= self._len:
        raise IndexError('list index out of range')

    if idx < len(self._lists[0]):
        return 0, idx

    _index = self._index

    if not _index:
        self._build_index()

    pos = 0
    child = 1
    len_index = len(_index)

    while child < len_index:
        index_child = _index[child]

        if idx < index_child:
            pos = child
        else:
            idx -= index_child
            pos = child + 1

        child = (pos << 1) + 1

    return (pos - self._offset, idx)

不用看那堆异常处理，直接看循环部分。当 idx 小于左子树大小时进左子树找，否则减去左子树大小并进右子树找，这和 BST 的查询操作是一致的。我们来分析一下复杂度，不妨设我们分了 bb 块，那么满二叉树上的一条根链为 O(log⁡b)O(\log b) 级别。当 b=O(n)b=O(\sqrt{n}) 时，查询复杂度为 O(log⁡n)O(\log n)。再来看看 _loc 函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def _loc(self, pos, idx):
    if not pos:
        return idx

    _index = self._index

    if not _index:
        self._build_index()

    total = 0

    # Increment pos to point in the index to len(self._lists[pos]).

    pos += self._offset

    # Iterate until reaching the root of the index tree at pos = 0.

    while pos:

       # Right-child nodes are at odd indices. At such indices
       # account the total below the left child node.

       if not pos & 1:
          total += _index[pos - 1]

          # Advance pos to the parent node.

       pos = (pos - 1) >> 1

   return total + idx

就是借助索引树来倍增跳。复杂度分析与上面相同，为 O(n)O(\sqrt{n})。写出 C++ 代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
std::pair<int, int> pos(int idx) {
    if (idx < (int) lists[0].size()) return std::make_pair(0, idx);
    if (index.empty()) build_index();
    int p = 0, n = index.size();
    for (int i = 1; i < n; i = p << 1 | 1) {
        if (idx < index[i]) p = i;
        else idx -= index[i], p = i + 1;
    } return std::make_pair(p - offset, idx);
}

int loc(int pos, int idx) {
    if (pos == 0) return idx;
    if (index.empty()) build_index();
    int tot = 0;
    for (pos += offset; pos; pos = (pos - 1) >> 1) {
        if (!(pos & 1)) tot += index[pos - 1];
    } return tot + idx;
}

插入

找到 add 函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def add(self, value):
    _lists = self._lists
    _maxes = self._maxes

    if _maxes:
        pos = bisect_right(_maxes, value)

        if pos == len(_maxes):
            pos -= 1
            _lists[pos].append(value)
            _maxes[pos] = value
        else:
            insort(_lists[pos], value)

            self._expand(pos)
    else:
        _lists.append([value])
        _maxes.append(value)

    self._len += 1
  • 首先当块链为空时，直接在末尾加入即可。
  • 否则我们二分找到 val 所属块。这里 bisect_right 的行为类似于 std::upper_bound，返回下标。
    • 若 val 无后继，说明它直接放到最后一个块的末尾即可，同时更新块内最值。
    • 否则，在块内插入 val，并且维护块链性质。

写出 C++ 版代码：

1
2
3
4
5
6
7
8
9
10
void add(const T& val) {
    if (!maxes.empty()) {
        int pos = std::upper_bound(maxes.begin(), maxes.end(), val) - maxes.begin();
        if (pos == (int) maxes.size()) pos--, lists[pos].emplace_back(val), maxes[pos] = val;
        else lists[pos].insert(std::upper_bound(lists[pos].begin(), lists[pos].end(), val), val);
        expand(pos);
    } else {
        lists.emplace_back(1, val), maxes.emplace_back(val);
    } len++;
}

expand 操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def _expand(self, pos):
    _load = self._load
    _lists = self._lists
    _index = self._index

    if len(_lists[pos]) > (_load << 1):
        _maxes = self._maxes

        _lists_pos = _lists[pos]
        half = _lists_pos[_load:]
        del _lists_pos[_load:]
        _maxes[pos] = _lists_pos[-1]

        _lists.insert(pos + 1, half)
        _maxes.insert(pos + 1, half[-1])

        del _index[:]
    else:
        if _index:
            child = self._offset + pos
            while child:
                _index[child] += 1
                child = (child - 1) >> 1
            _index[0] += 1

这个函数有两条逻辑。首先当块长大于二倍 load 时，执行分裂操作，把这块从中间分成两块，然后清空索引树（这里一定要清空，本蒟蒻被这个卡了 4h）。不分裂且建好索引树时，我们把这个块到根节点链上的值都加一。C++ 版如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
void expand(int pos) {
    if ((int) lists[pos].size() > (load << 1)) {
        std::vector<T> half(lists[pos].begin() + load, lists[pos].end());
        lists[pos].erase(lists[pos].begin() + load, lists[pos].end());
        maxes[pos] = lists[pos].back();
        lists.insert(lists.begin() + pos + 1, half);
        maxes.insert(maxes.begin() + pos + 1, half.back());
        index.clear();
    } else if (!index.empty()) {
        for (int i = offset + pos; i; i = (i - 1) >> 1) index[i]++;
        index[0]++;
    }
}

删除

找到 discard 函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def discard(self, value):
    _maxes = self._maxes

    if not _maxes:
        return

    pos = bisect_left(_maxes, value)

    if pos == len(_maxes):
        return

    _lists = self._lists
    idx = bisect_left(_lists[pos], value)

    if _lists[pos][idx] == value:
        self._delete(pos, idx)

在二分找到 value 后调用了 _delete 函数，找到它：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def _delete(self, pos, idx):
    _lists = self._lists
    _maxes = self._maxes
    _index = self._index

    _lists_pos = _lists[pos]

    del _lists_pos[idx]
    self._len -= 1

    len_lists_pos = len(_lists_pos)

    if len_lists_pos > (self._load >> 1):
        _maxes[pos] = _lists_pos[-1]

        if _index:
            child = self._offset + pos
            while child > 0:
                _index[child] -= 1
                child = (child - 1) >> 1
                _index[0] -= 1
     elif len(_lists) > 1:
        if not pos:
            pos += 1

        prev = pos - 1
        _lists[prev].extend(_lists[pos])
        _maxes[prev] = _lists[prev][-1]

        del _lists[pos]
        del _maxes[pos]
        del _index[:]

        self._expand(prev)
    elif len_lists_pos:
        _maxes[pos] = _lists_pos[-1]
    else:
        del _lists[pos]
        del _maxes[pos]
        del _index[:]

一个大分讨的结构：

  • 若块长大于一半的 load，更新块内的最大值，然后把在索引树上把该块到根节点的路径值减一；
  • 否则，若块数大于 11，将该块合并到上一块，若当前块为第一块就合并到下一块。由于这样完了也会导致块长大于二倍 load，执行 expand 操作；
  • 否则，若删除此元素后列表不为空，直接维护块内最大值；
  • 否则，清空列表。

C++ 实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
bool erase(const T& val) {
    if (maxes.empty()) return false;
    int pos = std::lower_bound(maxes.begin(), maxes.end(), val) - maxes.begin();
    if (pos == (int) maxes.size()) return false;
    int idx = std::lower_bound(lists[pos].begin(), lists[pos].end(), val) - lists[pos].begin();
    if (lists[pos][idx] != val) return false;

    lists[pos].erase(lists[pos].begin() + idx), len--;
    int n = lists[pos].size();
    if (n > (load >> 1)) {
        maxes[pos] = lists[pos].back();
        if (!index.empty()) {
            for (int i = offset + pos; i; i = (i - 1) >> 1) index[i]--;
            index[0]--;
        } 
    } else if (lists.size() > 1) {
        if (!pos) pos++;
        int pre = pos - 1;
        lists[pre].insert(lists[pre].end(), lists[pos].begin(), lists[pos].end());
        maxes[pre] = lists[pre].back();
        lists.erase(lists.begin() + pos), maxes.erase(maxes.begin() + pos);
        index.clear(), expand(pre);
    } else if (n > 0) {
        maxes[pos] = lists[pos].back();
    } else {
        lists.erase(lists.begin() + pos), maxes.erase(maxes.begin() + pos);
        index.clear();
    } return true;
}

查询第 kk 小

kth 操作在 Python 里是重载的 [] 运算符，找到 __getitem__ 函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
def __getitem__(self, index):
    _lists = self._lists

    if isinstance(index, slice):
        start, stop, step = index.indices(self._len)

        if step == 1 and start < stop:
            # Whole slice optimization: start to stop slices the whole
            # sorted list.

            if start == 0 and stop == self._len:
                return reduce(iadd, self._lists, [])

            start_pos, start_idx = self._pos(start)
            start_list = _lists[start_pos]
            stop_idx = start_idx + stop - start

            # Small slice optimization: start index and stop index are
            # within the start list.

            if len(start_list) >= stop_idx:
                return start_list[start_idx:stop_idx]

            if stop == self._len:
                stop_pos = len(_lists) - 1
                stop_idx = len(_lists[stop_pos])
            else:
                stop_pos, stop_idx = self._pos(stop)

            prefix = _lists[start_pos][start_idx:]
            middle = _lists[(start_pos + 1):stop_pos]
            result = reduce(iadd, middle, prefix)
            result += _lists[stop_pos][:stop_idx]

            return result

        if step == -1 and start > stop:
            result = self._getitem(slice(stop + 1, start + 1))
            result.reverse()
            return result

        # Return a list because a negative step could
        # reverse the order of the items and this could
        # be the desired behavior.

        indices = range(start, stop, step)
        return list(self._getitem(index) for index in indices)
    else:
        if self._len:
            if index == 0:
                return _lists[0][0]
            elif index == -1:
                return _lists[-1][-1]
        else:
            raise IndexError('list index out of range')

        if 0 <= index < len(_lists[0]):
            return _lists[0][index]

        len_last = len(_lists[-1])

        if -len_last < index < 0:
            return _lists[-1][len_last + index]

        pos, idx = self._pos(index)
        return _lists[pos][idx]

前面那一大坨是 Python 的切片索引，不用管它。就是用 pos 函数找到哪个块和块内索引直接返回即可。C++ 实现：

1
2
3
4
T operator[] (int idx) {
    auto pir = pos(idx);
    return lists[pir.first][pir.second];
}

查询排名

Python 里有两种排名：bisect_left 和 bisect_right，对应 C++ 中的 std::lower_bound 与 std::upper_bound。我们找到这两个东西：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def bisect_left(self, value):
    _maxes = self._maxes

    if not _maxes:
        return 0

    pos = bisect_left(_maxes, value)

    if pos == len(_maxes):
        return self._len

    idx = bisect_left(self._lists[pos], value)
    return self._loc(pos, idx)

def bisect_right(self, value):
    _maxes = self._maxes

    if not _maxes:
        return 0

    pos = bisect_right(_maxes, value)

    if pos == len(_maxes):
        return self._len

    idx = bisect_right(self._lists[pos], value)
    return self._loc(pos, idx)

用对应的二分函数找到哪个块和它在块内的位置，用 loc 函数转换。C++ 实现：

1
2
3
4
5
6
7
8
9
10
11
12
int lower_bound(const T& val) {
    if (maxes.empty()) return 0;
    int pos = std::lower_bound(maxes.begin(), maxes.end(), val) - maxes.begin();
    if (pos == (int) maxes.size()) return len;
    return loc(pos, std::lower_bound(lists[pos].begin(), lists[pos].end(), val) - lists[pos].begin());
}
int upper_bound(const T& val) {
    if (maxes.empty()) return 0;
    int pos = std::upper_bound(maxes.begin(), maxes.end(), val) - maxes.begin();
    if (pos == (int) maxes.size()) return len;
    return loc(pos, std::upper_bound(lists[pos].begin(), lists[pos].end(), val) - lists[pos].begin());
}

基于这个东西，我们可以用 upper_bound(x) - lower_bound(x) 来实现计数功能。加点剪枝：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int count(const T& val) {
    if (maxes.empty()) return 0;
    int l = std::lower_bound(maxes.begin(), maxes.end(), val) - maxes.begin();
    if (l == (int) maxes.size()) return 0;
    int r = std::upper_bound(maxes.begin(), maxes.end(), val) - maxes.begin();
    int x = std::lower_bound(lists[l].begin(), lists[l].end(), val) - lists[l].begin();
    if (r == (int) maxes.size()) return len - loc(l, x);
    int y = std::upper_bound(lists[r].begin(), lists[r].end(), val) - lists[r].begin();
    if (l == r) return y - x;
    return loc(r, y) - loc(l, x);
}
bool contains(const T& val) {
    if (maxes.empty()) return false;
    int pos = std::lower_bound(maxes.begin(), maxes.end(), val) - maxes.begin();
    if (pos == (int) maxes.size()) return false;
    int idx = std::lower_bound(lists[pos].begin(), lists[pos].end(), val) - lists[pos].begin();
    return lists[pos][idx] == val;
}

这样我们就实现了一个功能比较完整的有序列表了。

复杂度分析

首先设我们分成了 bb 块。

在修改时，分裂合并由均摊分析可得，总复杂度不超过 O(n)O(n)。而更新索引树是 O(log⁡b)O(\log b) 的。瓶颈在插入删除为 O(b)O(b)。但是众所周知 std::vector 的插入删除常数很小，在 10610^6 数据下约是 1500\dfrac{1}{500} 级别，因此我们可以认为 O(b)O(b) 跑的比 O(log⁡b)O(\log b) 还快，这样复杂度就是 O(log⁡n)O(\log n) 了。Sorted Containers 文档里也是这么写的：

1
2
3
"""
Runtime complexity: `O(log(n))` -- approximate.
"""

对于查询操作，二分显然是 O(log⁡b)O(\log b) 的，而 pos 和 loc 都在 O(log⁡b)O(\log b) 层的索引树上操作，复杂度也是 O(log⁡n)O(\log n)。由均摊分析，建立索引树的次数不超过 O(b)O(b) 次。

因此，你可以认为索引树优化块状链表的整体复杂度为 O(log⁡n)O(\log n)。

不知道这个东西能不能可持久化。

模板

这是一份完整的 sorted_vector 模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
template <class T>
struct sorted_vector {
private:
	static constexpr int DEFAULT_LOAD_FACTOR = 340;
	int len, load, offset;
	std::vector<std::vector<T>> lists;
	std::vector<T> maxes, index;
	
	void expand(int pos) {
		if ((int) lists[pos].size() > (load << 1)) {
			std::vector<T> half(lists[pos].begin() + load, lists[pos].end());
			lists[pos].erase(lists[pos].begin() + load, lists[pos].end());
			maxes[pos] = lists[pos].back();
			lists.insert(lists.begin() + pos + 1, half);
			maxes.insert(maxes.begin() + pos + 1, half.back());
			index.clear();
		} else if (!index.empty()) {
			for (int i = offset + pos; i; i = (i - 1) >> 1) index[i]++;
			index[0]++;
		}
	}
	
	std::vector<int> parent(const std::vector<int>& a) {
		int n = a.size();
		std::vector<int> res(n >> 1);
		for (int i = 0; i < (n >> 1); i++) res[i] = a[i << 1] + a[i << 1 | 1];
		return res;
	}
	void build_index() {
		std::vector<int> row0;
		for (const auto& v : lists) row0.emplace_back(v.size());
		if (row0.size() == 1) return index = row0, offset = 0, void();
		std::vector<int> row1 = parent(row0);
		if (row0.size() & 1) row1.emplace_back(row0.back());
		if (row1.size() == 1) {
			index.emplace_back(row1[0]);
			for (int i : row0) index.emplace_back(i);
			return offset = 1, void();
		}
		int dep = 1 << (std::__lg(row1.size() - 1) + 1), u = row1.size();
		for (int i = 1; i <= dep - u; i++) row1.emplace_back(0);
		std::vector<std::vector<int>> tree = {row0, row1};
		while (tree.back().size() > 1) tree.emplace_back(parent(tree.back()));
		for (int i = tree.size() - 1; i >= 0; i--) index.insert(index.end(), tree[i].begin(), tree[i].end());
		offset = (dep << 1) - 1;
	}
	
	std::pair<int, int> pos(int idx) {
		if (idx < (int) lists[0].size()) return std::make_pair(0, idx);
		if (index.empty()) build_index();
		int p = 0, n = index.size();
		for (int i = 1; i < n; i = p << 1 | 1) {
			if (idx < index[i]) p = i;
			else idx -= index[i], p = i + 1;
		} return std::make_pair(p - offset, idx);
	}
	
	int loc(int pos, int idx) {
		if (pos == 0) return idx;
		if (index.empty()) build_index();
		int tot = 0;
		for (pos += offset; pos; pos = (pos - 1) >> 1) {
			if (!(pos & 1)) tot += index[pos - 1];
		} return tot + idx;
	}
public:
	sorted_vector() : len(0), load(DEFAULT_LOAD_FACTOR), offset(0) {}
	int size() const {return len;}
	bool empty() const {return maxes.empty();}
	
	void clear() {
		len = 0, offset = 0;
		lists.clear(), maxes.clear(), index.clear();
	}
	
	void add(const T& val) {
		if (!maxes.empty()) {
			int pos = std::upper_bound(maxes.begin(), maxes.end(), val) - maxes.begin();
			if (pos == (int) maxes.size()) pos--, lists[pos].emplace_back(val), maxes[pos] = val;
			else lists[pos].insert(std::upper_bound(lists[pos].begin(), lists[pos].end(), val), val);
			expand(pos);
		} else {
			lists.emplace_back(1, val), maxes.emplace_back(val);
		} len++;
	}
	
	bool erase(const T& val) {
		if (maxes.empty()) return false;
		int pos = std::lower_bound(maxes.begin(), maxes.end(), val) - maxes.begin();
		if (pos == (int) maxes.size()) return false;
		int idx = std::lower_bound(lists[pos].begin(), lists[pos].end(), val) - lists[pos].begin();
		if (lists[pos][idx] != val) return false;
		
		lists[pos].erase(lists[pos].begin() + idx), len--;
		int n = lists[pos].size();
		if (n > (load >> 1)) {
			maxes[pos] = lists[pos].back();
			if (!index.empty()) {
				for (int i = offset + pos; i; i = (i - 1) >> 1) index[i]--;
				index[0]--;
			} 
		} else if (lists.size() > 1) {
			if (!pos) pos++;
			int pre = pos - 1;
			lists[pre].insert(lists[pre].end(), lists[pos].begin(), lists[pos].end());
			maxes[pre] = lists[pre].back();
			lists.erase(lists.begin() + pos), maxes.erase(maxes.begin() + pos);
			index.clear(), expand(pre);
		} else if (n > 0) {
			maxes[pos] = lists[pos].back();
		} else {
			lists.erase(lists.begin() + pos), maxes.erase(maxes.begin() + pos);
			index.clear();
		} return true;
	}
	
	T operator[] (int idx) {
		auto pir = pos(idx);
		return lists[pir.first][pir.second];
	}
	
	int lower_bound(const T& val) {
		if (maxes.empty()) return 0;
		int pos = std::lower_bound(maxes.begin(), maxes.end(), val) - maxes.begin();
		if (pos == (int) maxes.size()) return len;
		return loc(pos, std::lower_bound(lists[pos].begin(), lists[pos].end(), val) - lists[pos].begin());
	}
	int upper_bound(const T& val) {
		if (maxes.empty()) return 0;
		int pos = std::upper_bound(maxes.begin(), maxes.end(), val) - maxes.begin();
		if (pos == (int) maxes.size()) return len;
		return loc(pos, std::upper_bound(lists[pos].begin(), lists[pos].end(), val) - lists[pos].begin());
	}
	int count(const T& val) {
		if (maxes.empty()) return 0;
		int l = std::lower_bound(maxes.begin(), maxes.end(), val) - maxes.begin();
		if (l == (int) maxes.size()) return 0;
		int r = std::upper_bound(maxes.begin(), maxes.end(), val) - maxes.begin();
		int x = std::lower_bound(lists[l].begin(), lists[l].end(), val) - lists[l].begin();
		if (r == (int) maxes.size()) return len - loc(l, x);
		int y = std::upper_bound(lists[r].begin(), lists[r].end(), val) - lists[r].begin();
		if (l == r) return y - x;
		return loc(r, y) - loc(l, x);
	}
	bool contains(const T& val) {
		if (maxes.empty()) return false;
		int pos = std::lower_bound(maxes.begin(), maxes.end(), val) - maxes.begin();
		if (pos == (int) maxes.size()) return false;
		int idx = std::lower_bound(lists[pos].begin(), lists[pos].end(), val) - lists[pos].begin();
		return lists[pos][idx] == val;
	}
};

如果要自定义比较顺序，需要重载运算符。

应用

理论上这种优化方法适用于所有块状链表。所以这里放几个块链题：