对 AVL 树的扩展应用

前言

AVL 树是工程中常用的平衡树，其在大量查询方面具有优势。然而，AVL 树在 OI 中却没有特别地位。

笔者认为，AVL 树原理简单，比 OI 常用平衡树快很多，码量也不是很大。本文探究 AVL 树在 OI 领域的扩展应用。

AVL 树原理

AVL 的每个节点维护一个 high 域，表示子树的高度。AVL 需要维护 ∣highl−highr∣≤1|high_l-high_r|\le 1。

左旋右旋的引入

注意到，对一棵 BST 结构进行调整是不影响树的合法性的。举个例子：

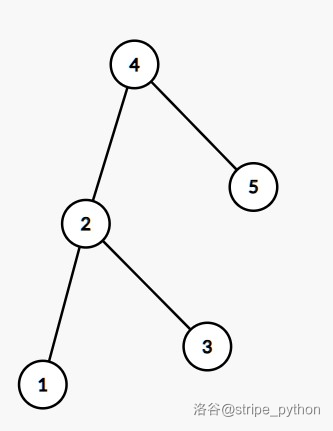
这棵 BST 可以调整为：

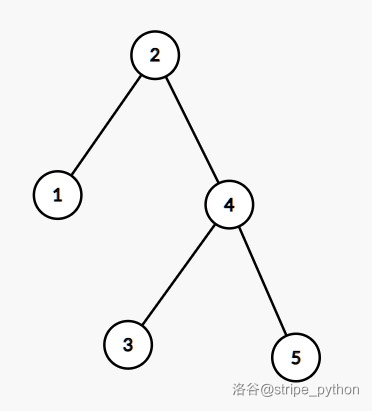
这就是平衡树的左旋操作。类似地，把上述调整的逆过程称作右旋。

参考代码：

1
2
3
4
5
6
7
8
9
10
static node* left_rotate(node* p) {
    node *q = p->left;
    p->left = q->right, q->right = p, p->pushup();
    return q->pushup();
}
static node* right_rotate(node* p) {
    node *q = p->right;
    p->right = q->left, q->left = p, p->pushup();
    return q->pushup();
}

如何维护平衡

分类讨论破坏平衡的情况：

  1. LL 型（左孩子的左孩子过深），如图：

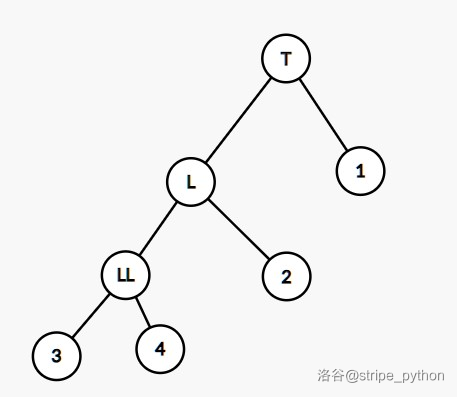
解法：右旋节点 TT。

  1. RR 型（右孩子的右孩子过深），解法：类似 LL 型，左旋节点 TT。

  2. LR 型（左孩子的右孩子过深），如图：

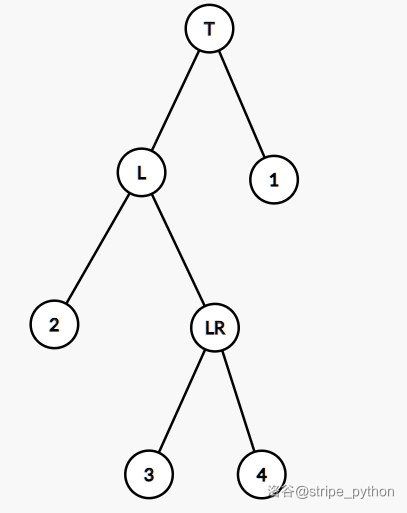
    解法：左旋节点 L，成为 LL 型，后右旋节点 T，即左右双旋。

  3. RL 型（右孩子的左孩子过深），解法：类似 LR 型，右旋节点 RR 后左旋节点 TT，即右左双旋。

双旋的参考实现：

1
2
3
4
5
6
7
8
static node* left_right_rotate(node* p) {
    p->left = right_rotate(p->left);
    return left_rotate(p);
}
static node* right_left_rotate(node* p) {
    p->right = left_rotate(p->right);
    return right_rotate(p);
}

参考实现

AVL 完整实现

可持久化

这部分内容摘自 本蒟蒻的题解。

原理介绍

既然有旋 Treap 可持久化，同样使用旋转维护平衡的 AVL 树也可以可持久化。

每一次旋转、插入、删除时，我们复制一份 AVL 节点，见代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
static node* left_rotate(node* p) {
    // 左旋节点 p
    node *q = p->left;
    p->left = copy(p->left);   // Added
    p->left = q->right, q->right = p, p->pushup();
    return q->pushup();
}
static node* right_rotate(node* p) {
    // 右旋节点 p
    node *q = p->right;
    p->right = copy(p->right);   // Added
    p->right = q->left, q->left = p, p->pushup();
    return q->pushup();
}

参考实现

可持久化 AVL 完整实现

文艺平衡树

原理介绍

思考一下 Splay 树如何实现文艺平衡树。

做法是把 al−1a_{l-1} splay 到根，再把 ar+1a_{r+1} splay 到根的右孩子。则 ar+1a_{r+1} 的左节点就代表这段区间。

由于 AVL 树高为严格 O(log⁡n)O(\log n)，可以使用类 Splay 操作把节点旋转到根。为了维护平衡，还需要把节点转回去，需要 44 次类 Splay，但是很难写常数还大。